Contents
1. Several models to choose from
Passive sampler calibration is often done by exposing samplers to a constant concentration of target compounds (Cw), followed by fitting the accumulated amounts to a kinetic model. In many cases it can be assumed that the accumulation rate (dN/dt) is linearly proportional to the effective concentration difference between the water and the sampler.
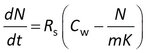
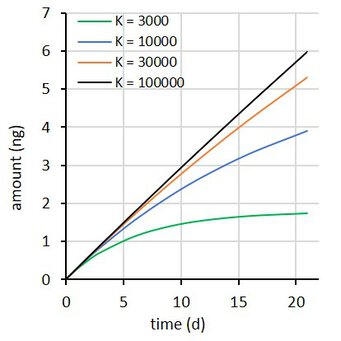
where Rs is the water sampling rate, Cw is the concentration in water, m the sorbent mass, and K the sorbent-water sorption coefficient. This is a first order differential equation. Sampling rate models predict that the difference between the initial and the final concentration in the sampler decays exponentially with time (at constant Cw). Some examples are shown at the right for compounds with K = 3×103 to 1×105 L/kg, with Cw = 2 ng/L, sorbent mass = 0.0003 kg, and sampling rate (Rs) = 0.15 L/d.
Several variants of passive sampling rate model fits exist.
Model 1: Rs – K model
The model that is easiest to interpret has the water sampling rate (Rs) and the sorption coefficient (K) as adjustable parameters.
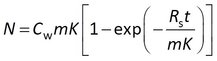
This model is sometimes expressed differently, depending on the data processing prior to statistical analysis. Some researchers model the concentration in the sampler (Cs) instead of the amount, and divide both sides of the above equation by the sorbent mass m
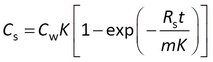
Others first express the data as a concentration factor CF = Cs/Cw
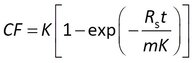
In all of these cases the accumulation data are modeled with Rs and K as adjustable parameters.
Model 2: ke – K model
Although model 1 can be fitted to experimental data directly (e.g., R-project, Matlab, and other), some statistics software requires basic transformations in order to match the model with the built-in equations. A frequently used transformation is to write the group Rs /(mK) as a rate constant ke.
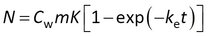
This model can be written in terms of Cs and CF as above, and in addition it can be noted that the accumulated amounts reach a plateau value of N∞ = CwmK at equilibrium
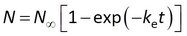
This is the ”one-phase association” standard model in Graphpad Prism. After fitting the data, Rs is obtained from ke by
Rs = m K ke
and K is evaluated from
K = N∞/(mCw)
A difference with Model 1 is that K and ke are treated as independent adjustable parameters in the curve fitting. This causes some difficulties because ke is inversely proportional to K.
Model 3: asymptotic regression model (ABQ model)
Townsend et al. (2018) included an initial amount N0 in model 2, and rearranged this model to
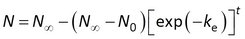
The accumulation data could then be fitted to GenStat’s standard asymptotic regression function
N = A + B Qt
A = N∞
B=-( N∞ – N0)
Q = exp(-ke)
After fitting the data to the model, Rs is obtained from
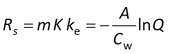
and K is calculated from
K = A/(mCw)
A difference with model 2 is that an additional parameter is needed (3 instead of 2), and that Q = exp(−ke) rather than ke is used as an adjustable parameter. The parameters A = N∞ and Q =exp(−ke) are negatively associated in this model (higher K means higher A and lower Q).
2. Rs and K estimates
A challenge with all three models is how to estimate the parameters when the uptake is essentially linear. This happens when the sorption coefficient is very high (black and amber lines in figure above). A further challenge with models 2 and 3 is that Rs is obtained indirectly: from ke and K for model 2, and from A and Q for model 3. This may (or may not) result in lower accuracy of the estimated Rs values.
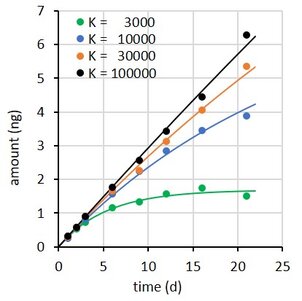
The performance of the models was therefore evaluated by simulating the uptake of three compounds over a time period of 21 d.
Accumulated amounts were calculated from model 1, with K between 3×103 and 1×105 L/kg, Cw = 2 ng/L, m = 0.0003 kg, and Rs = 0.15 L/d, for 8 exposure times up to 21 d.
A the end of the exposure period the amounts were 97, 65, 30, and 10% of their equilibrium values. For each compound 100 uptake experiments were simulated by adding 5% random noise to the amounts. See adjacent plot for some examples.
Parameters were estimated for models 1, 2, and 3 using weighted nonlinear least squares analysis (R-project, nls function). Parameters were also estimated using Excel’s Solver Add-In (Billo, 2001).
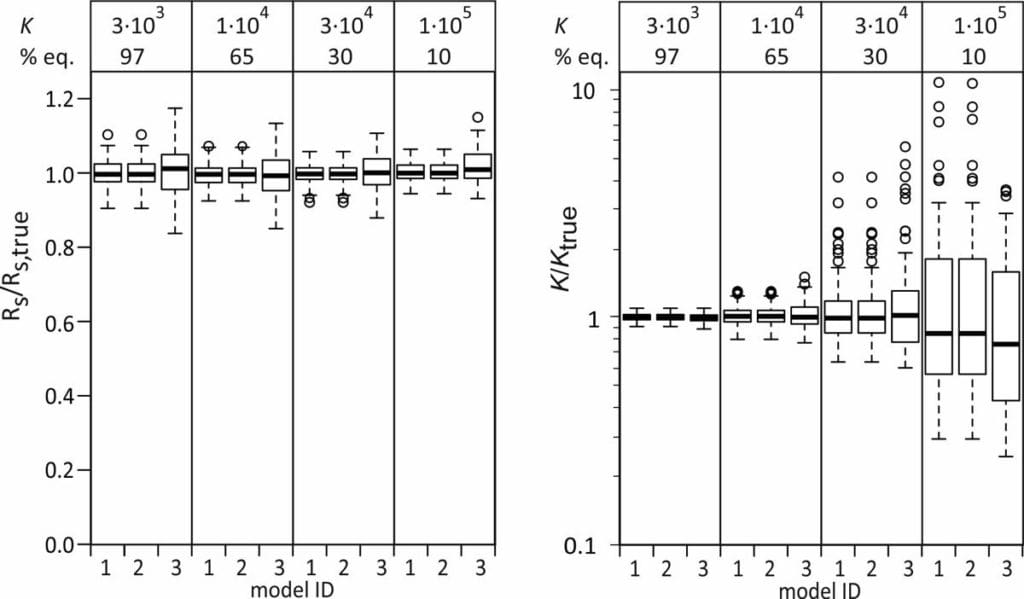
Ratios of estimated and true Rs were close to 1 for all models and all model compounds, even though the Rs estimates from models 2 and 3 were obtained indirectly. The Rs estimates from model 3 show a slightly larger scatter.
Median ratios of estimated and true K values are also close to 1 for all three models. The scatter in the K/Ktrue ratios is larger for the more linear uptake data, as expected.
3. Uncertainty estimates in Rs and K
Nonlinear least squares analysis includes estimation of the standard errors in the adjustable parameters. Rs is estimated directly with model 1, but is calculated from two other parameters with model 2 (Rs = m K ke ) and model 3 (Rs = -[A lnQ]/Cw). The usual method for estimating standard errors in calculated values is error propagation under the assumption that the estimated parameters are uncorrelated. The standard error sRs is then given for model 2 as
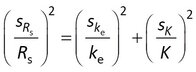
where ske and sK are the standard errors in ke and K.
Assuming that the error in Cw can be neglected, sRs for model 3 is obtained from
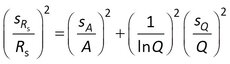
where sA and sQ are the standard errors in A and Q.
Standard errors in the sorption coefficient (sK) are obtained directly from the nonlinear least squares output of model 2, and for model 3 sK is given by
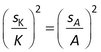
To test the validity of these error estimates, the predicted standard errors in Rs and K for individual model runs (spredicted) were compared with the observed standard errors within each set of 100 runs (sobserved).
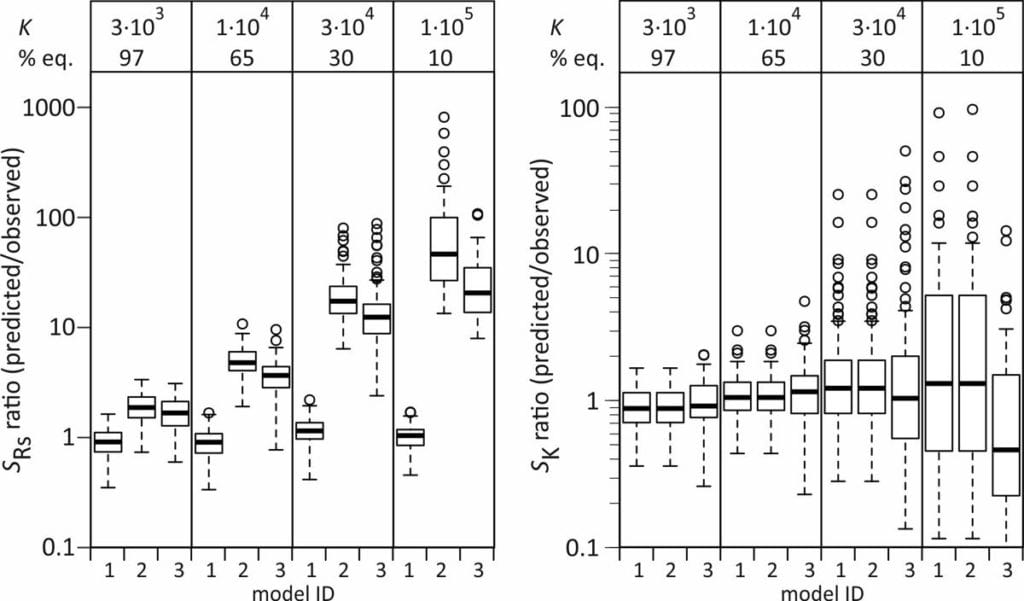
Standard errors in Rs are well-predicted with model 1, but are overestimated with models 2 and 3, also for the compound that reaches 97% equilibrium. Standard errors in K are on average well predicted by all three models, but (naturally) show a large scatter for the compounds that reach a small degree of equilibrium during the exposure.
Better estimates of sRs from models 2 and 3 can be obtained by accounting for the covariance between ke and K (model 2) or A and Q (model 3), but this increases the computational burden, and using model 1 is a more straightforward approach.
4. Choosing nonlinear versus linear least-squares
Nonlinear least squares analysis yields the correct Rs, even when the uptake is essentially linear (see Rs/Rs,true plot above). A practical approach for selecting linear versus nonlinear least squares is to select the method that yields the smallest residual errors. A visual inspection of plots with experimental values and model fit, and a comparison of Rs estimates and standard errors from linear and nonlinear least squares suffices. Alternatively, a partial F-test can be used to check if the nonlinear model (two parameters) gives a significantly better fit than the linear model (one parameter).
Nonlinear least squares estimations do not always converge when the uptake is linear. In those cases the linear model can be selected, again after checking the plots with measured and modeled data.
5. Optimal passive sampling rate model fit
- All three nonlinear models yield similar values of Rs and K
- Only model 1 gives a realistic estimate of the standard error in Rs.
- Choosing between nonlinear and linear model is not very critical. The choice can be based on visual inspection of plots of modeled and experimental data, or on a partial F-test.
6. Free template for the Rs – K model
An excel template for estimation of Rs and K can be downloaded for free. It is easy to operate, and comes with a manual including screenshots.
Basic features are
- estimates of Rs and K for 10 data sets in one run
- standard errors of Rs and K
- comparison with linear regression results
- partial F-test for choosing nonlinear versus linear modeling
- plots of residual errors
- plots of data + model fit
- weighted and unweighted nonlinear regression
- no macro’s; no security issues
- up to 20 data points per experiment
7. Need to test a different model?
PaSOC is happy to adapt the free passive sampling rate model fit template according you your needs.
- Include a lag phase
- Change the dependent variable from amount to concentration in the sorbent (Cs = N/m) or concentration factor (CF = Cs/Cw)
- Optimize logK instead of K
- Any other modification
Click How we work for further details.
References
Billo, E.J., 2001. Non-linear regression using the solver. In: Excel for Chemists: A Comprehensive Guide. John Wiley & Sons, Inc., New York, pp. 223–238.
Townsend, I., Jones, L., Broom, M., Gravell, A., Schumacher, M., Fones, G.R., Greenwood, R., Mills, G.A., 2018. Calibration and application of the Chemcatcher® passive sampler for monitoring acidic herbicides in the River Exe, UK catchment. Environ. Sci. Pollut. Res. 25, 25130–25142. https://doi.org/10.1007/s11356-018-2556-3
… and embedded URLs in the text